PPS-23-ScalaSim

Implementazione del Sistema

Assegnazione del lavoro

Di seguito le iniziali dei cognomi dei membri saranno affiancate ad ogni capitolo per il quale si ritiene/ritengono maggiormente responsabile/i gli studenti coinvolti.

V → Vincenzi Fabio
I → Iorio Matteo
F → Furi Stefano
Implementazione del Sistema
- Cellular Automaton V-I-F
  - Cell I-F
    - State I-F
  - Rule F
    - Domain Specific Language per la costruzione di NeighbourRule F
- Environment I-V
  - Configurazione tramite Mixin I
  - Space I-F
  - Tipologie di Space I
- Engine I
- Interfaccia Grafica V
- Simulazioni V-I-F
  - Conway’s Game of Life V
  - Brian’s Brain V
  - Langton’s Ant F
  - WaTor I-F

In generale, tutti i componenti del gruppo hanno lavorato cooperando e in maniera simultanea allo sviluppo dell’intera parte del modello di base del simulatore.

All’intero di questo capitolo verranno descritte le modalita attraverso la quale sono state definite le varie classi, gli eventuali problemi riscontrati ed infine le modalita attraverso la quale queste difficolta sono state risolte.

Cellular Automaton

Uno dei primi concetti che e stato sviluppato, riguarda il Cellular Automaton. Le classi sviluppate per la realizzazione del Cellular Automaton, sono diverse e possono essere elencate qui di seguito:

Cellular Automaton
Dimension
Cell
Neighbour
Rule

Le seguenti classi qui sopra elencate, ad esclusione di Dimension, sono racchiuse all’intero del package: domain.automaton, dove al suo interno sono contenute tutte le componenti software a supporto del concetto di automa cellulare.

Dal momento in cui esistono diverse categorie di Cellular Automaton, tra cui una specifica categoria la quale per un singolo stato di una Cell potrebbero venire applicate piu di una regola contemporaneamente, si e deciso di utilizzare un type parameter per la definizione della struttura dati nella quale andare a memorizzare le diverse regole che compongono il Cellular Automaton. A supporto di questa funzionalita inoltre si e deciso di implementare, tramite l’utilizzo di mixin, diverse strutture dati gia funzionanti da utilizzare per memorizzare lavorare su tali regole.

Di seguito sono presentate le classi che ritieniamo siano degne di un approfondimento implementativo, rispetto a quanto precedentemente descritto nel capitolo di design.

Cell

Uno dei componenti fondamentali per un Cellular Automaton e il concetto di Cell. La realizzazione di questo componente ha previsto la definizione di un nuovo trait denominato Cell, tale trait e definito generico nella dimensione dal momento in cui una Cell deve far riferimento ad una dimensionalita dello spazio generica, per definire cio e stato necessario forzare il parametro generico come sotto classe del trait Dimension. In questo modo si ha la garanzia che Cell ed Cellular Automaton facciano riferimento allo stesso tipo di dimensione dello spazio.

Una delle componenti principali di Cell e la posizione che assumoe nello pazio, rappresentato dal valore position, Tale posizione e definita anch’essa generica nella dimensione D dello spazio. Inoltre la Cell e caratteriizzata da uno stato che ha in un preciso istante di tempo. Per modellare lo stato e stato definito un nuovo parametro denominato state di tipo State.

trait Cell[D <: Dimension]:
    def position: Position[D]
    def state: State
object Cell:
    def apply[D <: Dimension](p: Position[D], s: State): Cell[D] = CellImpl(p, s)
    def unapply[D <: Dimension](cell: Cell[D]): Option[(Position[D], State)] = Some((cell.position, cell.state))
    private case class CellImpl[D <: Dimension]
      (override val position: Position[D], override val state: State)
    extends Cell[D]

Dopo la definizione del trait si e passati allo sviluppo dell’object Cell il cui compito e quello di fornire una factory per le Cell. Oltre a ciò è stata definita una case class che implementasse il trait Cell, in modo da fornire una sua implementazione da utilizzare durante lo sviluppo delle simulazioni.

State

Nella maggior parte dei casi, la definizione di uno stato è semplicemente rappresentata da un product type, ossia un’enumerazione. Per altri casi, come per esempio gli stati dell’automa cellulare WaTor, è necessario mantenere un’insieme di informazioni all’interno di uno stato. In questo modo, lato Environment non si dev’essere a conoscenza dei dettagli implementativi dello stato (difatti trattato come un semplice State) e solo dal lato della definizione delle regole è possibile manipolare l’informazione trattenuta dallo stato.

Per questo motivo è stato esteso lo stato ad un generico stato con valore:

trait ValuedState[T]:
  def value: T
  def update(f: T => T): ValuedState[T] =
    val v: T = f(value)
    new ValuedState[T] { override def value: T = v }

Il valore trattenuto può rappresentare un qualsiasi oggetto, e una comoda funzione update permette di mantenere applicare una trasformazione al valore mantenuto, garantendo l’immutabilità degli oggetti.

Nota: l’impiego di tale stato richiede una corretta definizione di una funzione di comparazione tra gli stati. Essendo uno stato generico un’enumerazione, la funzione equals è sufficiente a discriminare stati diversi. Nel caso di un ValuedState potrebbe essere necessario escludere il valore trattenuto nell’atto di comparazione. Per esempio, per l’automa WaTor è stato definito un trait che permette di comparare solo grazie all’istanza della classe, e successivamente esteso per gli stati Shark e Fish:
sealed trait StateComparison:
  override def equals(x: Any) = x.getClass() == this.getClass()

Rule

Come già illustrato nel capitolo riguardante il Design, una Rule non è altro che l’applicazione di una funzione rispetto ad un particolare matcher. Ogni automa cellulare sviluppato per questo progetto, prevede l’impiego di una regola che si basi su vicinati, perciò il matcher sarà rappresentato da uno specifico State, e la funzione di trasformazione accetta in input un vicinato e restituisce il nuovo centro di quel vicinato. Negli automi cellulari che richiedono di modellare un concetto di movimento (i.e. Langton’s Ant e WaTor), si impiega la specializzazione MultipleOutputNeighbourRule, la quale restituisce sempre zero o due celle in output: la prima cella rappresenta la nuova cella dopo aver effettuato lo spostamento, mentre la seconda cella rappresenta la cella precedente lo spostamento.

Domain Specific Language per la costruzione di `NeighbourRule`

Essendo Rule il cuore di ogni automa cellulare, risulta necessario costruire meccanismi e astrazioni in grado di rendere la creazione di tali regole nella maniera più semplice e intuitiva possibile. Grazie alle capacità di Scala, è stato possibile define un Domain Specific Language (DSL) in grado di creare semplici NeighbourRule in maniera dichiarativa.

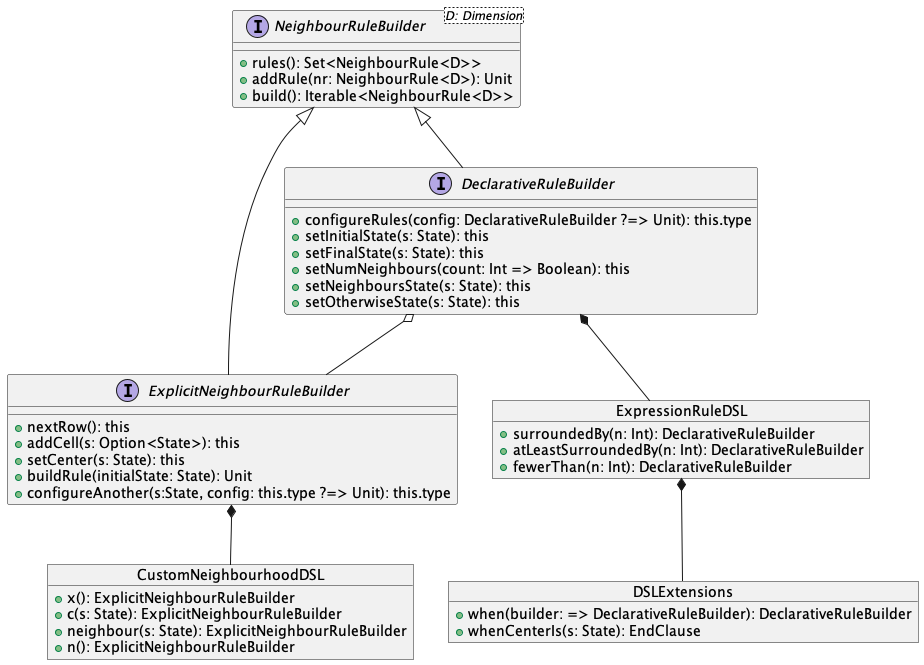
Diagramma UML delle classi componenti l'intero apparato del DSL per la crezione di NeighbourRule

In figura è illustrato come interagiscono tra di loro le componenti del DSL. Due specializzazioni sono state sviluppate di NeighbourRuleBuilder:

DeclarativeNeighbourRuleBuilder: permette la creazione di semplici regole costruendo predicati sulla cardinalità dei vicini aventi un certo stato.
ExplicitNeighbourRuleBuilder: costruisce NeighbourRule permettendo di specificare l’esatta configurazione che deve avere il vicinato.

Come suggerisce il nome, entrambe le componenti implementano il pattern Builder, ma la chiamata dei metodo del builder dovrebbe avvenire solo grazie agli oggetti che espongono il DSL vero e proprio.

Di seguito due esempi dell’impego delle due diverse modalità di costruzione delle regole.

DeclarativeRuleBuilder.configureRules:
  DEAD when fewerThan(2) withState ALIVE whenCenterIs ALIVE
  ALIVE when surroundedBy(2) withState ALIVE whenCenterIs ALIVE
  ALIVE when surroundedBy(3) withState ALIVE whenCenterIs ALIVE
  DEAD when atLeastSurroundedBy(4) withState ALIVE whenCenterIs ALIVE
  ALIVE when surroundedBy(3) withState ALIVE whenCenterIs DEAD

Nello snippet di codice sopra, vengono specificate le regole dell’automa Game of Life. Ogni riga contiene una specifica regola e ogni regola inizia con lo stato che assumerà l’automa in caso la regola venga applicata con successo. Successivamente, con la keyword when si può configurare la composizione del vicinato. Nell’esempio sopra, è illustrato come sia possibile specificare:

un limite superiore di vicini → fewerThan
un numero esatto di vicini → surroundedBy
un limite inferiore di vicini → atLeastSurroundedBy

Successivamente è quindi necessario specificare quale stato debbano avere i vicini, ed opzionalmente il raggio di ricerca dei vicini (keyword non mostrata nell’esempio withRadius, di default a 1 con vicinato di Moore). Successivamente, è opzionale specificare lo stato del centro per cui la regola venga applicata, ossia il matcher della regola. Se non viene specificato, la regola si riferisce a qualunque stato. È infine opzionale specificare uno stato alternativo (keyword otherwise al termine della regola) in caso in cui la regola non possa essere applicata per mancata corrispondenza con il vicinato. Se non viene specificato, il caso alternativo è costituito dal centro del vicinato in input inalterato.

Il DSL così dichiarato, permette di costruire un insieme di regole semplici adatte per modellare automi come Game of Life o Brian’s Brain.

È possibile inoltre costruire configurazioni custom di vicinati tramite un estensione del NeighbourRuleBuilder, impiegata attraverso composizione all’interno del DeclarativeRuleBuilder.

Come illustrato in figura, si considerino le regole che costituiscono l’automa Rule110.

Tramite l’impiego per composizione di ExplicitNeighbourRuleBuilder all’interno del builder dichiarativo è possibile specificare le regole in modo immediato tramite:

DeclarativeRuleBuilder.configureRules:
  White whenNeighbourhoodIsExactlyLike:
    neighbour(Black) | c(Black) | neighbour(Black)
  Black whenNeighbourhoodIsExactlyLike:
    neighbour(Black) | c(Black) | neighbour(White)
  Black whenNeighbourhoodIsExactlyLike:
    neighbour(Black) | c(White) | neighbour(Black)
  White whenNeighbourhoodIsExactlyLike:
    neighbour(Black) | c(White) | neighbour(White)
  Black whenNeighbourhoodIsExactlyLike:
    neighbour(White) | c(Black) | neighbour(Black)
  Black whenNeighbourhoodIsExactlyLike:
    neighbour(White) | c(Black) | neighbour(White)
  Black whenNeighbourhoodIsExactlyLike:
    neighbour(White) | c(White) | neighbour(Black)
  White whenNeighbourhoodIsExactlyLike:
    neighbour(White) | c(White) | neighbour(White)

Come per l’esempio precedente, una regola inizia sempre con lo stato che il centro del vicinato assumerà se la regola viene applicata con successo. Successivamente viene definito il vicinato attraverso la seguente sintassi:

neighbour(s: State): si specifica un vicino con lo stato in input. La sua posizione dipenderà dove verrà posizionato il centro all’interno della regola corrente;
c(s: State): posizionamento del centro della regola con stato iniziale pari allo stato dato in input (i.e. il matcher della regola);
|: separatore di celle;
x: placeholder per indicare un vicino da ignorare;
| n |: carattere di nuova linea.

L’intera sintassi può essere osservata con il seguente esempio:

DeclarativeRuleBuilder.configureRules:
  Alive whenNeighbourhoodIsExactlyLike:
    neighbour(Alive) | x       | neighbour(Alive) | n |
    x                | c(Dead) | x                | n |
    neighbour(Alive) | x       | neighbour(Alive)

dove, se il centro ha stato Dead e il suo vicinato assume il pattern indicato (vicini diagonali con stato Alive), allora il nuovo centro assumerà stato Alive.

Per la modellazione dell’automa cellulare Brian’s Brain, è possibile osservare gran parte della sintassi del DSL costruito:

DeclarativeRuleBuilder.configureRules:
  DYING whenNeighbourhoodIsExactlyLike(c(ON))
  ON when surroundedBy(2) withState ON whenCenterIs OFF otherwise OFF
  OFF whenNeighbourhoodIsExactlyLike(c(DYING))

Dopo aver costruito un DSL per la creazione regole di automa cellulare in maniera dichiarativa, è stata creato un semplice builder per automi cellulari che impiegano tale sintassi. In questo modo è possibile creare un semplice CellularAutomaton in uno spazio bidimensionale tramite:

CellularAutomatonBuilder.fromRuleBuilder:
  DeclarativeRuleBuilder.configureRules:
    dead when fewerThan(2) withState alive whenCenterIs(alive)
    alive when surroundedBy(2) withState alive whenCenterIs(alive)
    alive whenNeighbourhoodIsExactlyLike:
      neighbour(alive) | c(dead) | neighbour(dead)

Environment

Il secondo macro componente che e stato necessario sviluppare è l’Environment. Questo componente software incapsula lo spazio all’interno della quale vengono memorizzate le Cell di un Cellular Automaton. Per modellare questa astrazione nel tipo di simulazione che si vuole implementare, e stato necessario fare in modo che l’intero Environment fosse generico nel tipo di Cellular Automaton che si sta utilizzando. Per fare in modo di avere una rappresentazione generale dell’ambiente, è stato realizzato il trait GenericEnvironment, il quale è definito in due campi generici, il primo fa riferimento alla dimensione dello spazio della simulazione, mentre il secondo generico riguarda il tipo di ritorno dopo l’applicazione di una specifica regola.

trait GenericEnvironment[D <: Dimension, R] extends Space[D]:
  protected def saveCell(cells: Cell[D]*): Unit
  def applyRule(neighbors: Neighbour[D]): R

La definizione di questo Environment permette all’utente di applicare una determinata regola dato uno specifico Neighbour per poi sucessivamente salvare il risulato all’intero della struttura dati che si occupa di mantenere tutte le celle della simulazione.

Configurazione tramite Mixin

La modellazione dello spazio tramite il type ha reso possibile l’utilizzo dei Mixin. La configurazione della struttura dati con la quale modellare lo spazio e definito tramite uno o piu trait che vanno a comporre il Cake Pattern, attraverso il quale vengono configurate le diverse informazioni dell’Environment.

Questo meccanismo viene inoltre utilizzato per modellare la geometria dello spazio del Cellular Automaton. Ovvero ogni Cellular Automaton ha la propria concezione di spazio, ad esempio un semplice rettangolo, o uno spazio più complesso come quello toroidale. Anche per la modellazione di questo comportamento dell’Environment vengono utilizzati i Mixin attraverso cui è possibile specificare i diversi comportamenti riguardanti lo spazio geometrico ed inoltre le varie modalità con la quale percepire lo spazio stesso.

Space

Come formulato in precedenza, è fondamentale avere all’interno di una simulazione una strtuttura dati al cui interno vengono memorizzate tutte le Cell inerenti ad una simulazione. Per la rappresentazione di questo particolare aspetto si è sviluppato uno specifico trait all’interno di Environment denominato Space generico nella dimensione. La dimensione dello spazio e dell’automa cellulare sarà sempre la stessa dal momento in cui vengono definite tramite lo stesso generico in input all’Environment.

trait Space[D <: Dimension]:
   type Matrix
   def currentMatrix: Matrix
   def matrix: Matrix
   def neighbours(cell: Cell[D]): Neighbour[TwoDimensionalSpace]
   def dimension: Tuple
   protected def initialise(): Unit
   protected def availableCells(positions: Iterable[Position[D]]): Iterable[Cell[D]]

Dal momento in cui non è possibile sapere in anticipo il tipo di dimensione, la struttura dati all’interno della quale verranno memorizzate le Cell è definita tramite un type in questo modo l’utilizzatore avrà libera scelta nella tipologia di struttura dati da utilizare. Questo trait inoltre si occupa anche di andare a definire alcune operazioni di utility per lavorare sulla struttura dati utilizzata. Uno dei passaggi fondamentali per una qualsiasi simulazione riguarda l’inizializzazione dello spazio. Proprio per questo è stato definito il metodo initialise, al cui interno verrà definita lo stato iniziale della simulazione.

Tipologie di Space

Come descritto in precedenza, un automa cellulare ha il proprio spazio in cui evolve, lo spazio potrebbe essere rappresentato da un semplice rettangolo dimensionale, a forme molto più complesse come quelle di cubi e toroidi. Per rappresentare questa diversità di struttura dell’Environment sono stati definiti una serie di trait che possono rappresentare diverse strutture spaziali da utilizzare nella simulazione.

trait SquareEnvironment extends Space[TwoDimensionalSpace]:
    def side: Int
    override def dimension: Tuple2[Int, Int] = (side, side)
trait CubicEnvironment extends Space[ThreeDimensionalSpace]:
    def edge: Int
    override def dimension = (edge, edge, edge)
trait RectangularEnvironment extends Space[TwoDimensionalSpace]:
    def width: Int
    def heigth: Int
    override def dimension: Tuple2[Int, Int] = (heigth, width)
trait ToroidEnvironmnt extends RectangularEnvironment:
  extension (dividend: Int)
    infix def /%/(divisor: Int): Int = 
      val result = dividend % divisor
      result match
        case value if value < 0 => result + divisor
        case * => result

I trait qui sopra definiti permettono di modellare uno specifico Space da utilizzare per una simulazione. Questo tipo di modellazione permette di introdurre concetti specifici caratteristici per un certo tipo di Space, come nel caso di uno spazio toroidale il quale puo essere visualizzato come un rettangolo in uno spazio bidimensionale. Questo tipo di visione permette di introdurre specifici metodi da utilizzare per modellare lo spazio correttamente.

Engine

Similmente come per la componente Environment, la presenza di molteplici specializzazioni dei motori come mostrato nel capitolo di design serve per modellare al meglio il concetto di modularità e configurazione di uno specifico Engine. Il punto di partenza è il motore più generale e generico, il quale contiene al suo interno un Environment da poter interrogare e modificare in base all’evoluzione della simulazione. Successivamente vengono esposti metodi standard per interagire con il motore stesso, il quale dopo la chiamata del metodo start, effettuarà una serie di chiamate al metodo nextIteration il quale incapsula la logica di aggiornamento della griglia della simulaizone. Ad ogni iterazione inoltre, viene salvato lo stato della matrice corrente all’interno di una collezione di matrici, la quale rappresenta la storia della simulazione.

Tramite i mixin creati, come TimerEngine e ThreadEngine insieme alle specializzazioni in base al tipo di Environment, è possibile creare istanze che abbiano componenti “pluggabili” in base alle esigenze dello specifico motore. Di seguito un diagramma UML che riassume le classi generate e impiegate all’interno del simulatore.

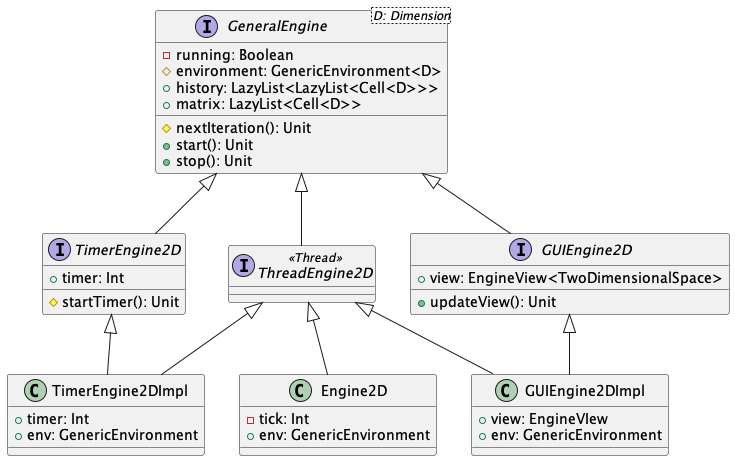
Diagramma UML delle Realizzazioni tramite mixin della componente `Engine`

Per via dei requisiti di prestazioni, tutte le istanze utilizzate includono come mixin sempre il trait ThreadEngine2D. Successivamente, ogni istanza implementa i concetti più specifici per il proprio ruolo.

Interazione `Engine` - `Environment`

Un’aspetto interessante riguarda la modalità con cui viene eseguita ogni iterazione. In prima battuta, la responsabilità di richiamare l’aggiornamento delle celle era delegata all’Engine stesso. In particolare, l’aggiornamento era richiamato come segue:

override def nextIteration: Unit = 
  environment().matrix
    .flatMap(_.map(cell => cell))
    .map(cell => env.applyRule(env.neighbours(cell)))
  saveInHistory

Per quanto questo approccio possa funzionare correttamente per la maggior parte delle simulaizoni, per tutte quelle simulazioni che necessitano di un processamento diverso (per esempio simulazioni che si compongono di precisi step di sense-decide-act), questo comporta una certa rigidità nel software, dovendo necessariamente costruire un ulteriore Engine adatto alle specifiche della simulazione.

Essendo una simulazione descritta da una specifica istanza di un CellularAutomaton e uno specifico Environment e tenendo in considerazione i fattori descritti precendentemente, la logica di aggiornamento della matrice è stata spostata nella classe responsabile della matrice stessa: Environment. Grazie a questa modifica, il motore ad ogni iterazione non farà altro che richiamare environment.nextIteration e salvare correttamente nella storia la matrice corrente, delegando completamente all’ambiente stesso l’implementazione della logica di aggiornamento. In questo modo, il comportamento di un automa cellulare può essere correttamente manipolato dall’ambiente in un modo corretto e, in caso di necessità, in modo custom.

Un esempio di un’automa cellulare che beneficia di questo cambiamento può essere l’automa Rule110, il quale invece che processare ogni singola cella dell’intera matrice, può interagire ad ogni step su una riga per volta, a partire da quella superiore, fino ad arrivare a quella inferiore. In questo modo, oltre a risparmiare una grande quantità di aggiornamenti, viene ottenuta una maggiore correttezza dell’automa stesso e il comportamento di esso risulta più predicibile.

Un’ulteriore automa che necessita di un comporamento custom per quanto riguarda l’aggiornamento delle celle è rappresentato dal modello di traffico di Biham-Middleton-Levin. Questo automa infatti prevede due tipologie di entità, le quali si muovono in modo alternato in base al numero corrente dell’iterazione (e.g. entità blu si muovono per numero di iterazioni pari, entità rosse per numero di iterazioni dispari).

Grazie a questa modifica quindi, la componente Engine risulta generale e indipendente verso il tipo di automa cellulare e il tipo di ambiente che esso necessità, rendendo future implementazioni di ulteriori automi completamente agnositiche verso il tipo di Engine impiegato.

Interfaccia Grafica

L’implementazione dell’interfaccia grafica è progettata per consentire agli utenti di configurare e visualizzare le simulazioni. L’interfaccia si basa su un’architettura dichiarativa e immutabile, utilizzando monadi e stati immutabili. Questo approccio garantisce una gestione coerente e prevedibile dello stato dell’interfaccia grafica.

SwingFunctionalFacade

Componente principale dell’interfaccia grafica, che fornisce un insieme di metodi per costruire e manipolare l’interfaccia tramite l’utilizzo di Swing. La facciata consente di creare frame, aggiungere bottoni, label, combo box, pannelli di pixel, input text e gestire la visualizzazione dei vari automi.

WindowState

La gestione dello stato della finestra è realizzata tramite WindowState, che definisce vari metodi per manipolare lo stato della finestra. Utilizzando la monade State, ogni operazione restituisce un nuovo stato della finestra senza modificare lo stato originale.

Esempio di utilizzo

val windowCreation = for
    _ <- setSize(1000, 600)
    _ <- addButton(text = "Start", name = "StartButton")
    _ <- addButton(text = "Stop", name = "StopButton")
    _ <- addButton(text = "Exit", name = "ExitButton")
    _ <- addComboBox(EnvironmentOption.options, "AutomatonsComboBox")
    _ <- show()
  yield

Video Exporter

MatrixToImageConverter

MatrixToImageConverter definisce un metodo per convertire una matrice di celle in un’immagine. Questo permette una facile estensione per diverse dimensioni e rappresentazioni dello spazio.

trait MatrixToImageConverter[D <: Dimension] {
  def convert(matrix: LazyList[Cell[D]], cellSize: Int, stateColorMap: Map[State, Color]): BufferedImage
}

SimpleMatrixToImageConverter rappresenta un implementazione specifica per uno spazio bidimensionale (TwoDimensionalSpace). Converte una matrice di celle in un’BufferedImage, utilizzando una mappa di colori per rappresentare gli stati delle celle.

VideoGenerator

VideoGenerator Definisce un metodo per generare un video da una sequenza di immagini.

trait VideoGenerator {
  def generate(videoFilename: String, images: Seq[BufferedImage], secondsPerImage: Double): Unit
}

JCodecVideoGenerator utilizza la libreria JCodec per creare un video. Converte una sequenza di immagini in un file video, dove ogni immagine viene visualizzata per un determinato numero di secondi.

Exporter

La classe Exporter coordina il processo di conversione della history di un automa cellulare in un video.

object Exporter {
  def exportMatrix[D <: Dimension, S <: State](engine: GeneralEngine[D], colors: Map[State, Color], converter: MatrixToImageConverter[D], videoGenerator: VideoGenerator, cellSize: Int, videoFilename: String, secondsPerImage: Double): Unit = {
    val images = engine.history.zipWithIndex.map { case (matrix, _) =>
      converter.convert(matrix, cellSize, colors)
    }.toList

    videoGenerator.generate(videoFilename, images, secondsPerImage)
  }
}

Simulazioni

Di seguito sono elencate le simulazioni sviluppate e presenti built-in all’interno del simulatore. Per ogni simulazione devono essere specificati:

L’ambiente della simulazione, dove in particolare è necessario specificare:
1. Come inizializzare l’ambiente;
2. La forma dei vicinati (e.g. Moore, VonNeumann o custom);
L’automa cellulare, composto semplicemente da un insieme di regole.

Conway’s Game of Life

Per la definzione dell’automa cellulare, è possibile specificare il suo comportamento tramite il builder.

def apply(): CellularAutomaton[TwoDimensionalSpace] =
  CellularAutomatonBuilder.fromRuleBuilder {
    DeclarativeRuleBuilder.configureRules:
      DEAD when fewerThan(2) withState ALIVE whenCenterIs ALIVE
      ALIVE when surroundedBy(2) withState ALIVE whenCenterIs ALIVE
      ALIVE when surroundedBy(3) withState ALIVE whenCenterIs ALIVE
      DEAD when atLeastSurroundedBy(4) withState ALIVE whenCenterIs ALIVE
      ALIVE when surroundedBy(3) withState ALIVE whenCenterIs DEAD
  }.build()

A questo punto l’ambiente definisce il vicinato come vicinato di Moore, e inizializza la matrice con un numero di celle con stato ALIVE pari al numero passato in input, mentre le rimanenti vengono imopostate a DEAD.

Brian’s Brain

Come per Game of Life, viene definito l’automa cellulare tramite il DSL nel seguente modo:

def apply(): CellularAutomaton[TwoDimensionalSpace] =
  CellularAutomatonBuilder.fromRuleBuilder {
    DeclarativeRuleBuilder.configureRules:
      DYING whenNeighbourhoodIsExactlyLike(c(ON))
      ON when surroundedBy(2) withState ON whenCenterIs OFF otherwise OFF
      OFF whenNeighbourhoodIsExactlyLike(c(DYING))
  }.build()

Similmente a Game of Life, la definizione dell’ambiente di Brian’s Brain prevede una forma del vicinato pari al vicinato di Moore, e l’inizializzazione della griglia avviene specificando un certo numero di celle ON e DYING, le restanti sono considerate OFF.

Langton’s Ant

Langton’s Ant, necessitando di un concetto di movimento tra le celle, fa impiego del tipo di regola MultipleOutputNeighbourRule. In particolare, l’output della regola sarà sempre composto da 2 celle: la prima rappresenta la cella di partenza prima di effettuare il movimento, mentre la seconda rappresenta la cella di arrivo dopo aver effettuato il movimento.

È possibile perciò definire il comportamento dell’automa come segue:

def antRule(n: Neighbour[TwoDimensionalSpace], moveCenterTo: RelativePositions): Iterable[Cell[TwoDimensionalSpace]] =
    val oldPositionState = n.center.state.asInstanceOf[ANT].cellColor.invert
    val direction = oldPositionState.invert match
      case WHITE => n.center.state.asInstanceOf[ANT].direction.clockWiseRotate
      case BLACK => n.center.state.asInstanceOf[ANT].direction.counterClockWiseRotate
    val newPosition = n.center.position.moveTo(direction)
    val newPositionState = n.neighbourhood.find(_.position == newPosition).get.state.asInstanceOf[CellState]

    Iterable(
      Cell(n.center.position, oldPositionState),
      Cell(newPosition, ANT(newPositionState, direction))
    )

In questo caso, esistono 2 stati per il colore delle celle della griglia e uno stato speciale per la rappresentazione della formica: in qualsiasi istante di tempo, lo stato ANT sarà sempre assegnato ad una ed una sola cella. Questo stato mantiente due ulteriori informazioni:

Il colore della cella sottostante la formica;
La direzione corrente della formica.

In questo modo, assegnando all’automa cellulare la regola per lo stato ANT, e una regola vuota per gli stati WHITE e BLACK, è possibile modellare correnttamente il comportamento di Langton’s Ant.

WaTor

WaTor rappresenta l’automa cellulare più complesso modellato per questo elaborato. Come per Langton’s Ant, esiste un concetto di movimento, ma in questo caso il movimento è previsto per tutte le celle attive (Fish e Shark).

In questo caso lo stato raffigura una specifica entità, e si definiscono Fish e Shark come estensioni di ValuedState. Per lo stato Fish è sufficiente assegnare al valore dello stato il chronon (contatore del numero di iterazioni in cui l’entità è sopravvissuta), mentre Shark necessita di portare con se anche l’informazione riguardante l’energia consumata o guadagnata durante il corso della simulazione.

Possiamo così riassumere la regola comportamentale delle entità Fish:

MultipleOutputNeighbourRule[TwoDimensionalSpace](Some(Fish())): n =>
  findRandomCellThat(n.neighbourhood)(_.state == Water) match
    case None => Iterable(incrementChronon(n.center))
    case Some(freeCell) => moveFishTo(n.center, freeCell)

Mentre per le entità Shark la logica risulta lievemente più complessa:

MultipleOutputNeighbourRule[TwoDimensionalSpace](Some(Shark())): n =>
  if n.center.state.asShark.value.energy == 0
  then Iterable(Cell[TwoDimensionalSpace](n.center.position, Water))
  else findRandomCellThat(n.neighbourhood)(_.state == Fish()) match
    case None => findRandomCellThat(n.neighbourhood)(_.state == Water) match
      case None => Iterable(incrementSharkStats(n.center))
      case Some(freeCell) => moveSharkTo(n.center, freeCell)
    case Some(fishCell) => moveSharkTo(n.center, fishCell, true)

dove la funzione moveXxxTo ha il compito di controllare se il chronon dell’entità ha raggiunto la soglia di riproduzione, e in caso positivo creare una nuova entità all’interno della cella di partenza prima del movimento. Inoltre, nel caso di moveSharkTo, viene rappresentato da un flag booleano se lo squalo, effettuando il movimento, mangia un pesce incrementandone quindi l’energia.

Indice

Capitolo Precedente

Capitolo Successivo

This site is open source. Improve this page.